本文主要记录在电子设计大赛训练时,做电源时需要对电路中某些输出量进行稳定控制,PID控制算法可以很好的实现该功能,其中增量式更符合对电源的电压电流量的控制。本文主要粗略对其进行介绍再使用Python实现一个电压输出稳定控制
以下仅限与对增量式PID控制算法的介绍,对于PID控制算法的概述(General Introduction)见“PID控制器入门概要”
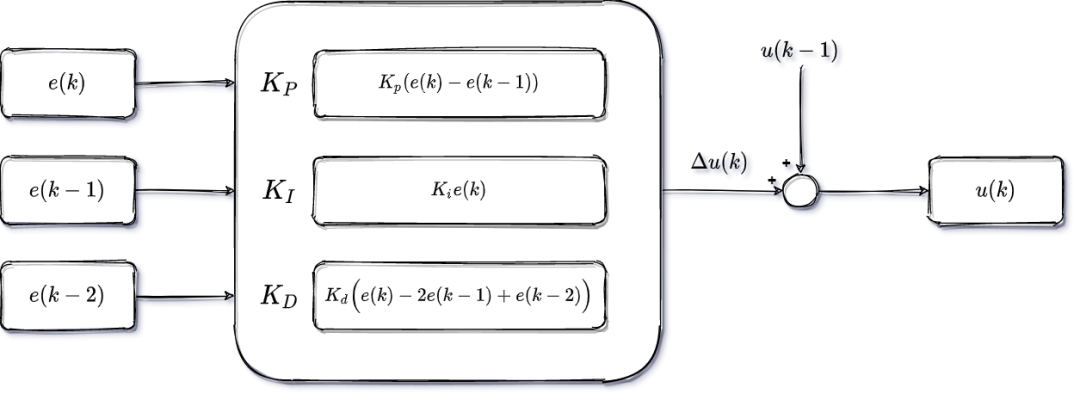
增量式PID控制将当前时刻的控制量和上一时刻的控制量做差,以差值为新的控制量,是一种递推式的算法。
其公式表示为:
Δ u ( k ) = K p ( e ( k ) − e ( k − 1 ) ) + K i e ( k ) + K d ( e ( k ) − 2 e ( k − 1 ) + e ( k − 2 ) ) (1) \Delta u(k) = K_p (e(k) - e(k-1)) + K_i e(k) + K_d(e(k) - 2e(k-1) + e(k-2)) \tag{1}
Δ u ( k ) = K p ( e ( k ) − e ( k − 1 ) ) + K i e ( k ) + K d ( e ( k ) − 2 e ( k − 1 ) + e ( k − 2 ) ) ( 1 )
其中:
K p K_p K p K i K_i K i K d K_d K d
因此若要使用增量式PID算法需要保存e ( k − 1 ) , e ( k − 2 ) e(k-1),e(k-2) e ( k − 1 ) , e ( k − 2 ) e ( k ) e(k) e ( k ) u ( k ) u(k) u ( k ) u ( k − 1 ) u(k-1) u ( k − 1 )
u ( k ) = u ( k − 1 ) + Δ ( k ) u(k) = u(k-1) + \Delta(k)
u ( k ) = u ( k − 1 ) + Δ ( k )
u ( k ) , u ( k − 1 ) , Δ u , e ( k ) , e ( k − 1 ) , e ( k − 2 ) u(k),u(k-1),\Delta u,e(k),e(k-1),e(k-2) u ( k ) , u ( k − 1 ) , Δ u , e ( k ) , e ( k − 1 ) , e ( k − 2 )
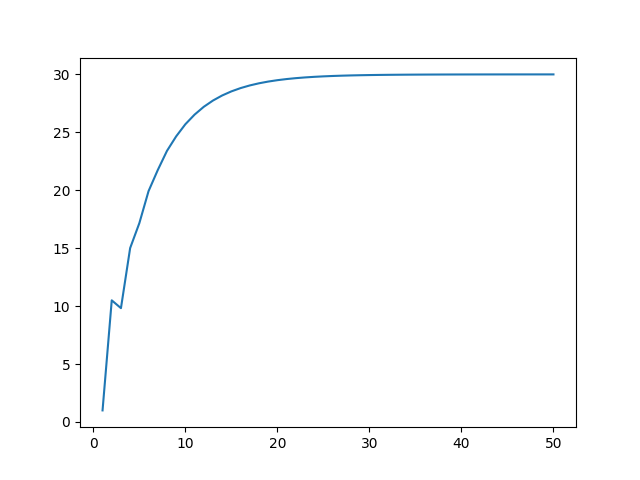
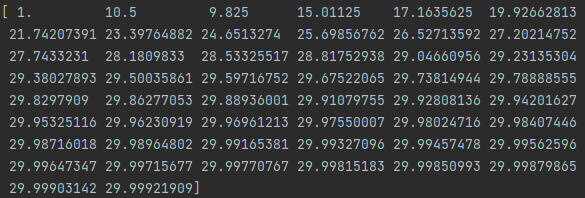
下面使用Python语言进行展示,得到输出曲线
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 import numpyimport pandasimport matplotlib.pyplotdef main ():30.0 0.0 0.05 0.2 0.1 0.0 0.0 range (1 , 50 , 1 )1.0 , 51.0 , 1.0 )for i in time:2 * e_k1 + e_k2)print (out)range (1 , 51 , 1 ), output)print (output)if __name__ == '__main__' :
通过不断改变K p , K i , K d K_p,K_i,K_d K p , K i , K d
当我在做DC-DC电源转换器直流稳压源时,发现由于系统反应过于迅速以至于转换器来不及反应导致系统无法达到预期目的,因此需要将参数调小并留有一定的系统反应时间。
在使用过程中我又对上述的PID计算代码进行了进一步封装,使用的时候可以向PID计算过程直接传递 Kp, Ki, Kd 参数,使用起来更为方便,且封装后的代码可以针对不同的过程使用,不必考虑其他问题,诸如:
变量的存储空间是否会相互影响
是否要考虑计算的内容是否为有特定单位的有意义的物理量
计算时的变量是否可见可读
代码封装之后,所有的PID计算全部进行了归一化,输出结果的范围为 [ − 1 , 1 ] [-1,1] [ − 1 , 1 ]
封装后的函数原型如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 float pidCalc (float Now_out, float Target, struct strPID Parameter ,float UpperLimit ,float LowerLimit) ;